1. Индексируемых величин, изменение которых должен отразить индекс.
2. Показателей, которые служат соизмерителями (весами).
Произведение индексируемой величины на соизмеритель (вес) должно давать определённую экономическую категорию (pq, Yq, tq и т.д.).
Правила построения агрегатных индексов:
1. Если строится индекс качественного показателя, то весами выступают показатели отчётного периода.
2. Если строится индекс количественного показателя, то весами выступают показатели базисного периода.
Агрегатный индекс стоимости продукции:
Ypq
,
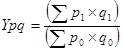где
0
×
q
0,
p
1
×
q
1
- стоимость произведённой продукции, соответственно в базисном и отчётном периодах.
Yq
- характеризует, изменение фактической стоимости произведённой продукции по анализируемому перечню:
Взаимосвязь:
Абсолютное изменение:
∆
pq
=
∑
p
1
×
q
1
─∑
p
0
×
q
0
∆
pq
=∆
pqp
+∆
pqq
Агрегатный индекс цен:
Yp
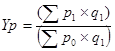, где
0
,
p
1- цена каждого вида продукции соответственно в базисном и в отчётном периодах.
q
1 -
объём каждого вида продукции в отчётном периоде.
Yp- характеризует, как изменились цены на различные виды продукции в среднем.
Взаимосвязь:
Абсолютное изменение:
∆
pqp
=
∑
p
1
×
q
1
─∑
p
0
×
q
1
Агрегатный индекс физического объёма:
Yq
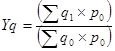, где
q
0
-
объём каждого вида продукции в базисном периоде.
Yq
- характеризует, как изменился в среднем общий объём продукции по анализируемому перечню:
Взаимосвязь:
Абсолютное изменение:
∆
pqq
=
∑
q
1
×
p
0
─∑
q
0
×
p
0
Средние индексы
- разновидность общих индексов, которые исчисляются как величина индивидуальных индексов (как средняя арифметическая или как средняя гармоническая).
Различают:
-Средний арифметический взвешенный индекс
- получается из агрегатного, если заменить в числителе значение индексируемого показателя отчётного периода равным ему произведением значения индивидуального индекса на значение индексируемой величины базисного периода.
Например: средний арифметический взвешенный индекс объёма продукции:
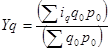, т.к.
, то 
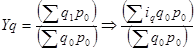
Применяется вместо агрегатных индексов количественных показателей.
-Средний гармонический взвешенный индекс
- получается также из агрегатного, только в знаменателе значение индексируемой величины базисного периода заменяется равным ей отношением значения индексируемой величины отчётного периода к значению индивидуального индекса.
Например: средний гармонический взвешенный индекс цены:
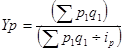, т.к.
, то 
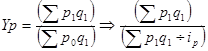
Применяется вместо агрегатных индексов качественных показателей.
Экономические явления часто характеризуются с помощью средних величин. В частности, все качественные показатели, как правило, выражаются в виде средних: средняя цена единицы продукции (
), средняя себестоимость единицы изделия (
), средняя заработная плата одного рабочего (
), выработка продукции в среднем па одного работника (
), средняя трудоемкость одного изделия (
) и т. п. Для изучения динамики таких показателей в статистической практике применяются индексы средних величин (средних уровней).
Читайте также >>>
Расчет экономической эффективности оптимизации электрического режима установки печь-ковш в условиях ККЦ ОАО ММК
В
данной работе осуществляется выбор организационно-правовой формы
Магнитогорского металлургического комбината (ММК), выбирается миссия для
предприятия, а также определяется экономический эффект от внедрения системы
оптимизации электрического режима УПК на учас ...
Расчет технико-экономических показателей электроцеха
Современное состояние и перспективы развития энергетики.
Чтобы получить энергию, необходимо затратить некоторое
количество энергетических ресурсов. Под энергетическими ресурсами понимают все
природные источники энергии, которые можно превращать в используемую ...